Hall measurements have long been a workhorse in condensed matter physics, offering a simple yet powerful way to probe electronic properties of materials. But as experiments increasingly venture into systems with mesoscopic spatial inhomogeneities, including, e.g., composition, magnetic domains, strain, and various moiré patterns, the interpretation of Hall measurements becomes less straightforward. A common assumption is that the measured Hall response from an inhomogeneous sample simply reflects an average of local Hall effects. But in reality, this is not always justified. Charge signals detected at the sample boundary are governed by global current paths and field distributions, which are shaped by the full spatial profile of the sample, not just its average properties.
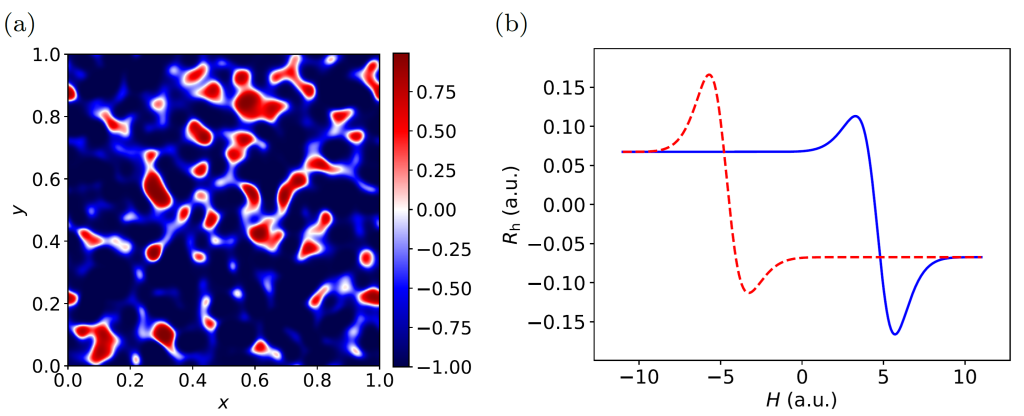
In a recent collaboration between physicists and mathematicians [1], we rigorously address this issue by deriving exact mathematical bounds on the global anomalous Hall conductivity (AHC) of inhomogeneous systems. Specifically, we prove that the measured Hall response must lie between the maximum and minimum values of the local anomalous Hall conductivity across the sample. This seemingly simple result provides a powerful diagnostic tool: Any apparent deviation of the measured signal outside this range can only arise from one of two possibilities—either the assumed local bounds are incorrect, or the measured quantity is not the true global anomalous Hall conductivity. Importantly, our framework allows for a clear classification of the often-debated Hall “hump” features (Figure below) observed during magnetic reversal in certain systems, distinguishing whether they originate from real topological effects (like skyrmions) or from magnetic and structral inhomogeneities.
We hope this work will serve as a robust anchor for interpreting future anomalous Hall experiments and perhaps inspire new ways of designing transport probes in magnetic materials.

Recent Comments